1. Collect a sample of persons who differ substantially in your dependent variable. Enter their data on that variable and on whatever independent variables you intend to use to provide prediction.
Example: Larry Hughes of Southern Illinois University provided Kyle Perkins with a set of diagnostic indicators for patients with Alzheimer's disease and similar debilitating conditions ranging from mild to severe. Each of these indicators was coded into an ordinal scale.
2. Anchor persons at their dependent variable values (ordinal or interval) and find the sub-set of independent variables which separates your sample of persons in the most stable and useful way.
Example: Anchor persons at their ordinal scale values: "Definitely Alzheimer's" = 2 logits, "Probably" = 1 logit, "Not" = 0 logit. Recode all variables so that score-to-measure correlations are positive. A factor analysis of the residuals from a Rasch analysis of all variables indicates which sub-set of independent variables cluster with the dependent variable, and so are most likely to predict it. Fine-tune this subset of clinical variables for clinical coherence, and to avoid accidental sample- specific relationships. ADL, MMSE and SBD remain.
3. Use this subset of independent variables to construct a predictor yardstick and to file a set of person measures.
Example: Unanchor the persons. Drop from the analysis the dependent and unwanted independent variables. Produce a file of person measures on ADL, MMSE, and SBD only. For convenience, logits are rescaled to provide an operational range of 0-100.
4. Anchor persons at your file of person measures and return all variables, including the dependent variable, to analysis to obtain calibrations for each item-step combination along your yardstick and also whatever qualifying statistics you find useful: estimation errors, fits, score-by-measure correlations. [Later, Ben simplified this by using zero-item-weights for the non-measurement variables.]
Example: The anchored person measures calibrate all variables onto one ruler, no matter how well they predict Alzheimer's. This step avoids problems with variable collinearity and the impact of accidental intra-sample correlations.
5. Craft a one page KEYMAPa to show the relative measure positions along your yardstick of diagnostically useful values of each predicting and predicted variable.
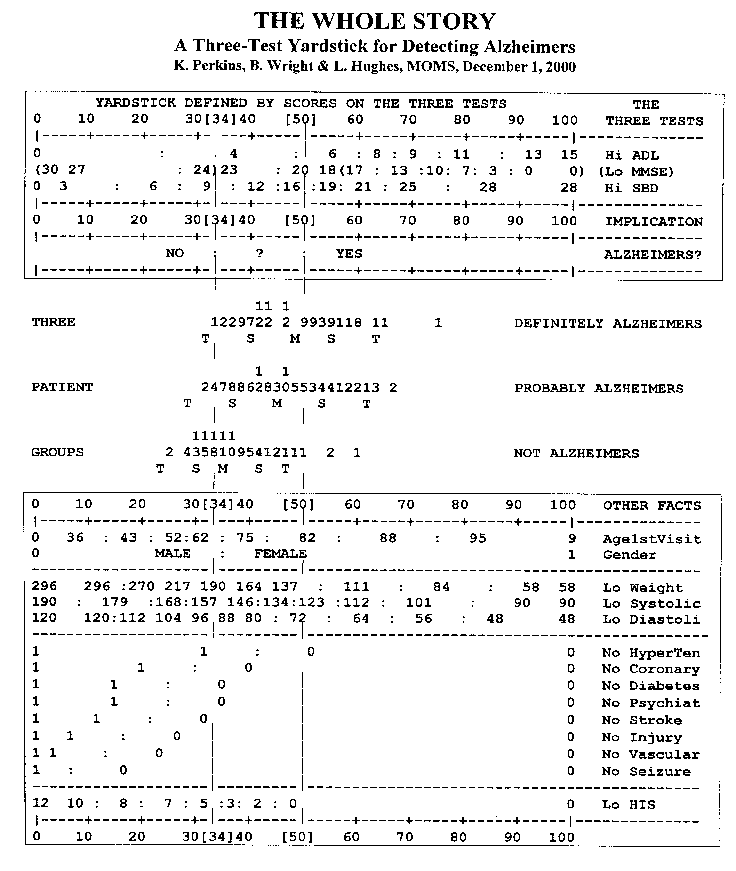
Example: In the Figure, the upper box predicts Alzheimer's. The dependent variable is shown below the independent predictor variables. The values in the box are the levels of the clinical indicators. In the Alzheimer's line, "?" is at 50% probability, the left ":" at 25% probability, the right ":" at 75% probability, according to the sample-distribution-free measurement model. The measurement regions for Alzheimer's diagnosis are thus 0-33 = "No", 34-50 = "?", 51-100 = "Yes", These accord with the current clinical levels on MMSE: 30-24, 23-18, and 17-0.
6. Stratify your persons into diagnostically useful levels of the original raw dependent variable and add the frequency distributions of person measures at each strata to your KEYMAP.
Example: These are between the boxes in the Figure.
7. The person distributions at each strata will diagram the predictive validity of your yardstick in detail and also expose possible challenges to the validity of some dependent variable values.
Example: The means, "M", of the strata show a clinically- meaningful advance: "Not", "Probably", "Definitely". The dispersions reflect diagnostic ambiguity. Outliers on each strata suggest the need for further evaluation of those patients, leading to amended diagnoses or the discovery of further relevant clinical indicators.
8. Yardstick positions of original values for independent variables not participating in yardstick construction will suggest how these other variables may contribute to your understanding of your dependent variable.
Example: The lower box suggests that obesity, high blood pressure, and other chronic or acute medical conditions mask or mitigate against the diagnosis of Alzheimer's. This box also confirms that Alzheimer's is more likely to afflict the elderly and women.
Benjamin D. Wright
The full paper is published in Hughes L.F., Perkins K., Wright B.D., Westrick H (2003) Using a Rasch scale to characterize the clinical features of patients with a clinical diagnosis of uncertain, probable or possible Alzheimer disease at intake. Journal of Alzheimer's Disease, 5, 5.
See also:
Rasch Measurement Instead of Regression. Benjamin D. Wright, Kyle Perkins, J. Kevin Dorsey. MULTIPLE LINEAR REGRESSION VIEWPOINTS. 2000 26(2) 36-41.
http://mlrv.ua.edu/2000/Vol26(2)/vol26(2).html
Multiple Regression with WINSTEPS: A Rasch Solution to Regression Confusion. Benjamin D. Wright. MULTIPLE LINEAR REGRESSION VIEWPOINTS. 2000 26(2) 42-45.
http://mlrv.ua.edu/2000/Vol26(2)/vol26(2).html

Rasch Regression: My Recipe. Wright, B.D. … Rasch Measurement Transactions, 2000, 14:3 p.758-9
| Forum | Rasch Measurement Forum to discuss any Rasch-related topic |
Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement
Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.
| Coming Rasch-related Events | |
|---|---|
| Jan. 16 - Feb. 13, 2025, Fri.-Fri. | On-line workshop: Rasch Measurement - Core Topics (E. Smith, Winsteps), www.statistics.com |
| Apr. 8 - Apr. 11, 2026, Wed.-Sat. | National Council for Measurement in Education - Los Angeles, CA, ncme.org/events/2026-annual-meeting |
| Apr. 8 - Apr. 12, 2026, Wed.-Sun. | American Educational Research Association - Los Angeles, CA, www.aera.net/AERA2026 |
| May. 15 - June 12, 2026, Fri.-Fri. | On-line workshop: Rasch Measurement - Core Topics (E. Smith, Winsteps), www.statistics.com |
| June 19 - July 25, 2026, Fri.-Sat. | On-line workshop: Rasch Measurement - Further Topics (E. Smith, Winsteps), www.statistics.com |
The URL of this page is www.rasch.org/rmt/rmt143u.htm
Website: www.rasch.org/rmt/contents.htm