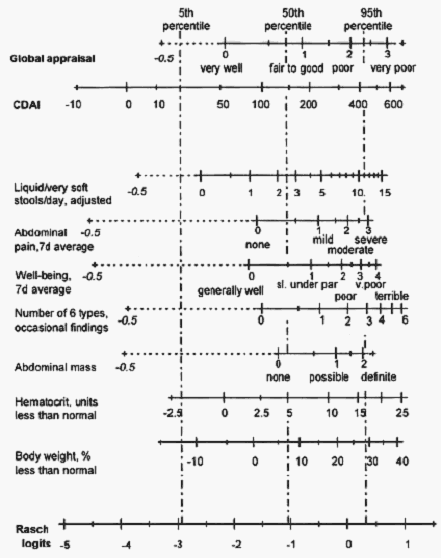
A Construct Map that Ben Wright Would Relish

This construct map of the "Crohn's Disease Activity Index" (CDAI) is Figure 11 in William R. Best, "A Rasch Model of the Crohn's Disease Activity Index (CDAI): Equivalent Levels of Ranked Attribute and Continuous Variable Scales", Chapter 5 in "Crohn's Disease: Etiology, Pathogenesis and Interventions", Jack N. Cadwallader (Ed.), Nova Publishers, 2008.

The map shows the relationship between the highly non-linear clinical indicators and the "Rasch logits" linear variable of "degree of sickness attributed to Crohn's Disease". Equal degrees of sickness align vertically on each of the clinical variables.

In a clinical setting, as soon as even one indicator variable has been observed, an estimate of the overall Rasch logit measure can be made. Observing more indicator variables refines the Rasch measure, but expensive, intrusive or time-consuming indicators are only required when high precision is needed for clinical decisions.

Changes in status across time can be tracked accurately in equal-interval Rasch logits, in the same way that weight or temperature can be tracked. The clinician's judgment is not misled by the non-linearity of the indicator variables.

Ben Wright discusses these maps further at "Rasch Regression - My Recipe", RMT 14:3, p. 758-9

www.rasch.org/rmt/rmt143u.htm

William Best summarizes the technical aspects of his analysis for RMT:

A partial credit Rasch model was developed from the original 112 patients' data used in the 1970s to develop the CDAI. For this model, continuous variables were condensed into variables of 6 ranked attributes each. Relationship of each of the nine component CDAI variables to Rasch logits is explored through scattergrams with jittered coincident points. Logic plus examination of these graphs indicate that best-fit scales should be smooth, monotonic, and with decreasing logit steps for equal interval variable steps. An origin-shifted logarithmic equation, encompassing observed ranges of a variable (X) and logit (Y), fits these specifications well; Y = a + b loge(X + c).

An objective in this effort is to juxtapose nine component CDAI scales and a single Rasch logit scale, so a viewer may appreciate equivalencies within observed ranges. This requires that the relationship between any two variables be the same in both directions. In conventional regression they are not. The curve that best describes equivalency between two scales is that passing through the same percentile values of those scales. Percentile is calculated as p=100(3i-1)/(3n+1), where i is rank and n is total.

Good fit to the origin-shifted logarithmic model is generally possible using three points, low, middle, and high. 5-50-95 percentiles were chosen for this sample, resulting in about 6 values in each tail. One cannot usually infer equal-interval relationships between values in ranked-attribute variables. However, assuming a continuous, unbounded distribution permits data manipulations not otherwise possible.

A simple model used here assigns integers to categories, 0 through k, with range, -0.5 to k+0.5. Zero implies a finding absent or at normal levels. Ties at any integer level, i, are then distributed uniformly between i-0.5 and i+0.5, rendering each percentile unique. Whether this approach is credible in any case depends on the face validity of resultant formulations.

An alternate approach for continuous variables is Deming regression, also producing a single relationship independent of direction. Ideally, one needs the error variance of each variable and computations are complex. However, assuming proportionate error is often intuitively appropriate and greatly simplifies computation.

I would welcome published reviews of this chapter.

William R. Best