Computer-adaptive testing: Dichotomous and Polytomous CAT:
A Bayesian Maximum-Falsification [maximum accuracy] approach
as an alternative to the usual Maximum-Information [maximum precision] approach

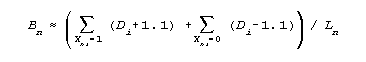
Note: Most CAT methods are based on "maximum information" - with rating scales these target respondents at the center of the rating scale. Essentially the central rating scale item difficulty substitutes for the dichotomous item difficulty as far as item selection is concerned, and www.rasch.org/rmt/rmt122q.htm is used for the estimation. Here is a CAT method based on "maximum falsification" - the tests are slightly longer, but yield a greater variety of expected responses. It is more complicated to operationalize, so start with the "maximum information" method, and if respondents say "this test is too bland", then switch to "maximum falsification".

Item selection and examinee measure estimation methods for computer-adaptive testing (CAT) have been motivated by the impractical and largely irrelevant goal of minimizing test length. In practice, there is little inefficiency or inconvenience associated with administering a few extra items to each examinee. In contrast, there is considerable benefit in administering longer tests in order to improve content balance and coverage, and to equalize item use.

A further benefit would be to implement CAT algorithms that are easy to check for correct operation and have face validity to non-specialists. The abstruse maximum-information item selection methods do not meet this need. A simpler Bayesian approach may serve. Its correct functioning is easy to verify, and it is also easy to explain in concrete, raw score terms.

Before we administer a dichotomous item, what performance level do we expect of examinees who will fail that item? Clearly we expect their performance to be nowhere near success, "1". But we would not administer the item to these examinees if we expected them to be clear failures, "0". So their expected performance level must be between "0" and "1", but on the failing side, less than "0.5". A Bayesian position could be that the expected performance of examinees who will fail an item is halfway between "0" and "0.5", say, 0.25 score points. Similarly, the expected performance for examinees who will succeed could be 0.75 score points.

From this standpoint, and in the absence of other information, our guess at the ability measure of examinees who succeed on an item is the measure corresponding to 0.75 score points on that item, i.e., 1.1 logits above that item's calibration. Since the information in 0.75 score points is 0.75*0.25, the variance of that one-item ability measure is 1/(0.75*0.25) = 5. Thus, after administering Ln dichotomous items to examinee n, that examinee's current ability estimate, Bn, can be approximated by the mean of the distribution of the one-item ability estimates:

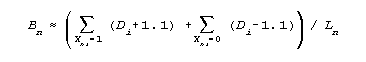
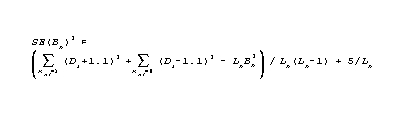
But a better estimate is the MLE estimate obtained by computing according to RMT 12:2 p. 638 (polytomies) or RMT 10:2 p. 449 (dichotomies)

This estimate of Bn selects the next item for administration. Only at the conclusion of the test is a more exact algorithm used to produce a more precise estimate and S.E. Indeed, more precise estimates may only be needed for examinees close to criterion levels.

This Bayesian approach extends to partial credit items. For a multiple category item, scored 0, 1, 2,.., k-1, k, the expected prior performance of those who score in the intermediate categories can correspond to the values of those categories. We expect examinees who score "1" to be "1"-level examinees, etc. We treat the extreme categories like dichotomies, so that the set of expected scores becomes 0.25, 1, 2,.., k-1, k-0.25. The logit values of these expected scores can be estimated for any CAT item with a calibrated partial credit scale and incorporated into the item bank.

After administering Ln partial credit items to examinee n, that examinee's current ability estimate, Bn can be approximated by:

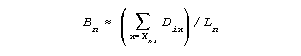
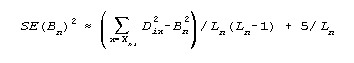
where Dix is the measure on item i corresponding to an expected score of x (using 0.25 when x=0, and k-0.25, when x=k, the top category.)

But a better estimate is the MLE estimate obtained by computing according to RMT 12:2 p. 638

With this approach, items are selected to give examinees the greatest opportunity to demonstrate their performance level. Item selection is based on score-level transitions, 0.5, 1.5, 2.5,..., k-1.5, k-0.5. Each successive response clarifies whether the examinee is performing higher or lower than currently estimated. The selection algorithm selects at random any item with a transition point near Bn. Transition points will border low scores on hard items and high scores on easy items. The Figure shows score-levels, their ability estimates, transition points and their difficulties for a typical item.

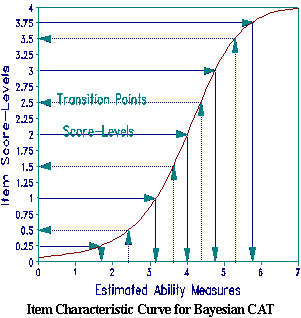
An alternative view of this approach is that it is an application of Carl Popper's Principle of Falsification. The test is continually challenging the examinee to falsify our previous measure estimate.

This CAT approach is motivated by the idea of a conversation about a person's problems, attitudes etc. The typical "maximum information" approach is like a talk with bureaucrat during which both participants are careful to avoid probing for, or asserting, extreme positions - a "politically correct" conversation. Everything is very safely in the middle of the rating scale. At the end of the test, the respondent can say "I answered all the questions truthfully, but I never told them what I really felt on the issues".  On a 5-category Lickert instrument, the ideal "maximum information" response would likely be "neutral" every time! And respondents quickly see the pattern, so response sets are encouraged!

Real conversations between intimates, and particularly real counselling sessions, probe the extremities. At the end of the administration, the respondent could say "I told them what I loved, what I hated, and what I didn't care about either way." The best item administration sequence would follow a substantive plan, going from the more superficial items to the more sensitive issues, but, in general, probably a uniform random selection from "falsification thresholds" would suffice. Of course, this method will perform worse statistically than the "maximum information" method - because it is designed to optimize the psychological results, not the statistical ones.

Computer-Adaptive Testing, CAT: A Bayesian approach. Linacre JM. … Rasch Measurement Transactions, 1995, 9:1 p.412

Rasch Publications
Rasch Measurement Transactions (free, online)	Rasch Measurement research papers (free, online)	Probabilistic Models for Some Intelligence and Attainment Tests, Georg Rasch	Applying the Rasch Model 3rd. Ed., Bond & Fox	Best Test Design, Wright & Stone
Rating Scale Analysis, Wright & Masters	Introduction to Rasch Measurement, E. Smith & R. Smith	Introduction to Many-Facet Rasch Measurement, Thomas Eckes	Invariant Measurement: Using Rasch Models in the Social, Behavioral, and Health Sciences, George Engelhard, Jr.	Statistical Analyses for Language Testers, Rita Green
Rasch Models: Foundations, Recent Developments, and Applications, Fischer & Molenaar	Journal of Applied Measurement	Rasch models for measurement, David Andrich	Constructing Measures, Mark Wilson	Rasch Analysis in the Human Sciences, Boone, Stave, Yale
in Spanish:	Análisis de Rasch para todos, Agustín Tristán		Mediciones, Posicionamientos y Diagnósticos Competitivos, Juan Ramón Oreja Rodríguez

Forum

Rasch Measurement Forum to discuss any Rasch-related topic

Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement

Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.

The URL of this page is www.rasch.org/rmt/rmt91d.htm

Website: www.rasch.org/rmt/contents.htm