PCA: Data Variance: Explained, Modeled and Empirical

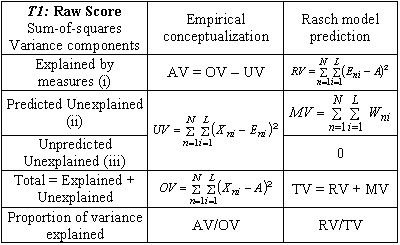
How much of the variance in my data do the Rasch measures explain? This is a crucial question, but its answer is far from obvious and can only be known approximately.

Here are three sources of variance in the data:

i) People differ in ability and items differ in difficulty. These cause different responses, and it is these differences that the Rasch measures are intended to reflect.

ii) People respond in an apparently random way, but still in accord with Rasch model predictions.

iii) People respond in a way that conflicts with Rasch model predictions.

Suppose that N people respond to L dichotomous items, scored 0, 1. The response by person n to item i is scored X_ni (using the notation of Wright & Masters, 1982, p. 100). Then the overall average response, A, is
.

So, conceptualizing the scored observations to be linear, as is typically done, the observed variance sum-of-squares, OV, in the data is
.

This includes (i), (ii) and (iii) above.

Once the Rasch ability measures {B_n} and difficulty measures {D_i} have been estimated, there is an expected value, E_ni, for each X_ni. The variance explained by the Rasch measures, RV, can then be expressed as:
corresponding to (i) above.

Associated with each E_ni is its Rasch-predicted model variance W_ni. Thus the variance not explained by the measures, but predicted by the Rasch model, MV, is
.

corresponding to (ii) above. The total variance in the data, TV, is predicted to be
TV = RV + MV.

When the data fit the Rasch model, then OV = TV.

Empirically, the unexplained variance, UV, is

corresponding to (ii) + (iii) above. Then, since fit to the model is never perfect, the variance actually explained, AV, a shown in Table T1, becomes
AV = OV - UV.

These variance computations can be extended to allow for missing data and polytomies by adjusting the summations.

When the data approximate the Rasch model, the proportion of variance explained is about equal for the two conceptualizations. When the data grossly misfit the model, the empirical variance explained by the measures, AV, can become negative. On the other hand, with anchored measures, the empirically unexplained variance can become less than the Rasch predicted variance, indicating overfit of the current data to the measures. Tables T1 and T2 show the algebraic components and also their values for the "Liking for Science" data.

T2: Raw Score Variance components in the "Liking for Science" data	Empirical conceptualization	Rasch model prediction
Explained by measures	AV = OV - UV = 564.63	RV = 562.70
Unexplained	UV = 543.92	MV = 546.48
Total = Explained + Unexplained	OV = 1108.55	TV = RV + MV = 1109.18
Proportion of variance explained	AV/OV = 51%	RV/TV = 51%

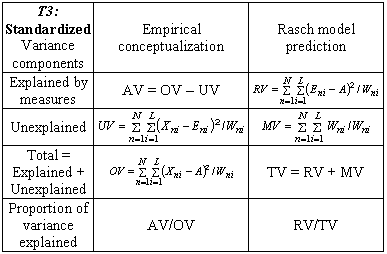
Variance in Standardized Units

An alternative conceptualization is in standardized units. Here each response is modeled to contribute one unit of statistical information. Consequently, the summations are in unit normal deviates rather than in raw scores. This is summarized in Table T3.

T4: Standardized Variance component in Winsteps Example 10A data	Empirical conceptualization	Rasch model prediction
Explained by measures	AV = OV - UV = 113.41	RV = 220.04
Unexplained	UV = 400.08	MV = 240.00
Total = Explained + Unexplained	OV = 513.49	TV = RV + MV = 460.04
Proportion of variance explained	AV/OV = 22%	RV/TV = 48%

It is followed by Table T4, a practical example for data noticeably contradicting the Rasch model. In this example of an MCQ test, 4 of 20 items have negative point-biserial correlations, i.e., are oriented in opposition to the Rasch dimension. This has reduced the variance explained by the Rasch dimension to half what would be expected were these data to fit the model.

Relationship to Principal Components Analysis (pCA) of Residuals (PCAR)

The variance "explained by the measures" corresponds to the Rasch dimension. The "unexplained" variance corresponds to all other dimensions and random noise. PCAR attempts to partition the unexplained variance based on factors representing other dimensions. This is done by decomposing the matrix of inter-item (or inter-person) correlations of residuals. In this matrix, each diagonal element is set to 1, indicating that there is one unit of residual variance contributed by each item (or person). Thus the total amount of variance to be explained by the PCAR, i.e., the sum of the factor eigenvalues, equals the number of items (or persons).

The "unexplained" variances in the Tables are in summed raw score or standardized units with little immediate meaning, so it is convenient to rescale them into eigenvalue units such that the Unexplained variance corresponds to the sum of the eigenvalues to be explained by the PCAR. This is shown in Table T5 using the Liking for Science data comprising 25 items.

T5: Standardized Variance Liking for Science	Empirical Eigenvalue units
Total = Explained + Unexplained	50.8 rescaled
Explained	25.8 rescaled
Unexplained	25.0 rescaled = PCAR
Explained by PCAR: 1st Factor 2nd Factor 3rd Factor	4.3 eigenvalue 2.9 eigenvalue 2.3 eigenvalue

The strength of the Rasch dimension, 25.8, can then be compared directly with the strength of the biggest secondary dimension, 4.3, indicating that, for most practical purposes, the Liking for Science data can be treated as unidimensional.

John M. Linacre

1. PCA: Data Variance: Explained, Modeled and Empirical
2. Critical Eigenvalue Sizes (Variances) in Standardized Residual Principal Components Analysis (PCA)
3. More about Critical Eigenvalue Sizes (Variances) in Standardized-Residual Principal Components Analysis (PCA)
4. Data Variance Explained by Rasch Measures
5. PCA: Variance in Data Explained by Rasch Measures

Data Variance: Explained, Modeled and Empirical, Linacre J.M. … Rasch Measurement Transactions, 2003, 17:3 p.942-943

Rasch-Related Resources: Rasch Measurement YouTube Channel
Rasch Measurement Transactions & Rasch Measurement research papers - free	An Introduction to the Rasch Model with Examples in R (eRm, etc.), Debelak, Strobl, Zeigenfuse	Rasch Measurement Theory Analysis in R, Wind, Hua	Applying the Rasch Model in Social Sciences Using R, Lamprianou	El modelo métrico de Rasch: Fundamentación, implementación e interpretación de la medida en ciencias sociales (Spanish Edition), Manuel González-Montesinos M.
Rasch Models: Foundations, Recent Developments, and Applications, Fischer & Molenaar	Probabilistic Models for Some Intelligence and Attainment Tests, Georg Rasch	Rasch Models for Measurement, David Andrich	Constructing Measures, Mark Wilson	Best Test Design - free, Wright & Stone Rating Scale Analysis - free, Wright & Masters
Virtual Standard Setting: Setting Cut Scores, Charalambos Kollias	Diseño de Mejores Pruebas - free, Spanish Best Test Design	A Course in Rasch Measurement Theory, Andrich, Marais	Rasch Models in Health, Christensen, Kreiner, Mesba	Multivariate and Mixture Distribution Rasch Models, von Davier, Carstensen
Rasch Books and Publications: Winsteps and Facets
Applying the Rasch Model (Winsteps, Facets) 4th Ed., Bond, Yan, Heene	Advances in Rasch Analyses in the Human Sciences (Winsteps, Facets) 1st Ed., Boone, Staver	Advances in Applications of Rasch Measurement in Science Education, X. Liu & W. J. Boone	Rasch Analysis in the Human Sciences (Winsteps) Boone, Staver, Yale	Appliquer le modèle de Rasch: Défis et pistes de solution (Winsteps) E. Dionne, S. Béland
Introduction to Many-Facet Rasch Measurement (Facets), Thomas Eckes	Rasch Models for Solving Measurement Problems (Facets), George Engelhard, Jr. & Jue Wang	Statistical Analyses for Language Testers (Facets), Rita Green	Invariant Measurement with Raters and Rating Scales: Rasch Models for Rater-Mediated Assessments (Facets), George Engelhard, Jr. & Stefanie Wind	Aplicação do Modelo de Rasch (Português), de Bond, Trevor G., Fox, Christine M
Exploring Rating Scale Functioning for Survey Research (R, Facets), Stefanie Wind	Rasch Measurement: Applications, Khine	Winsteps Tutorials - free Facets Tutorials - free	Many-Facet Rasch Measurement (Facets) - free, J.M. Linacre	Fairness, Justice and Language Assessment (Winsteps, Facets), McNamara, Knoch, Fan

Forum

Rasch Measurement Forum to discuss any Rasch-related topic

Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement

Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.

The URL of this page is www.rasch.org/rmt/rmt173g.htm

Website: www.rasch.org/rmt/contents.htm