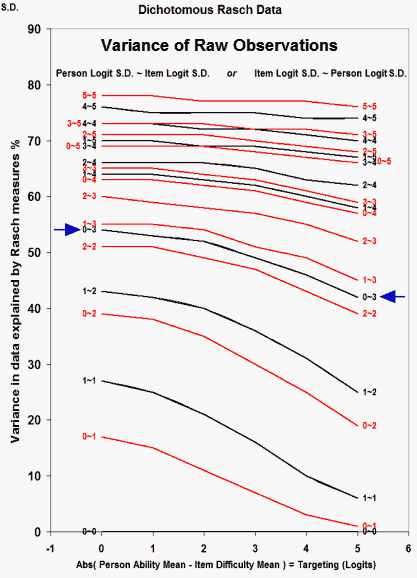
PCA: Variance in Data Explained by Rasch Measures

A Rasch model predicts that there will be a random aspect to the data. This is well understood. But what does sometimes surprise us is how large the random fraction is.

The Figure shows the proportion of raw-observation randomness predicted to exist in dichotomous observations under various conditions. Note (2015): Practical experience indicates that these curves are useable approximations for polytomous items.


The x-axis is the absolute difference between the mean of the person and item distributions, from 0 logits to 5 logits. The y-axis is the percent of variance in the data explained by the Rasch measures.

Each plotted line corresponds to one combination of standard deviations. The lesser of the person S.D. and the item S.D. is first, 0 to 5 logits, followed by "~". Then the greater of the person S.D. and the item S.D.

Thus, the arrows indicate the line labeled "0-3". This corresponds to a person S.D. of 0 logits and an item S.D. of 3 logits, or a person S.D. of 0 logits and an item S.D. of 3 logits. The Figure indicates that, with these measure distributions about 50% of the variance in the data is explained by the Rasch measures.

When the person and item S.D.s, are around 1 logit, then only 25% of the variance in the data is explained by the Rasch measures, but when the S.D.s are around 4 logits, then 75% of the variance is explained. Even with very wide person and item distributions with S.D.s of 5 logits only 80% of the variance in the data is explained.

For the unexplained variance, see Critical Eigenvalue Sizes (Variances) in Standardized Residual Principal Components Analysis (PCA).

In early versions of Winsteps, specify PRCOMP=R

How the Table was computed

This Table was produced with Excel:

  1. Normal distributions of logit measures for the items and persons were simulated using specified S.D.s and targeting (= mean difference between person measures and item measures).
  2. For each person-item combination were computed:
    the Rasch-dichotomous expected-score: Eni = 1/(1+exp(Di-Bn)
    and model-variance of the expected-score: Wni = Eni(1-Eni)
  3. The expected scores were averaged
  4. Sum-of-squares of explained variance is: sum[(expected score - average expected score)²]
  5. Sum-of-squares of unexplained variance is: sum( model-variances of expected scores )
  6. Explained variance = (Sum-of-squares of explained variance) / (Sum-of-squares of explained variance + Sum-of-squares of unexplained variance)

Here are some percentages for empirical datasets:

% Variance
Explained		DatasetWinsteps
File name
71.1%Knox Cube Testexam1.txt
29.5%CAT testexam5.txt
0.0%coin tossing-
25.8%Liking for Science(3 categories)example0.txt
37.5%NSF survey(3 categories)interest.txt
30.0%NSF survey(4 categories)agree.txt
78.7%FIM® (7 categories)exam12.txt

Please email me your own percentages to add to this list.

John Michael Linacre

Editor, Rasch Measurement Transactions

  1. PCA: Data Variance: Explained, Modeled and Empirical
  2. Critical Eigenvalue Sizes (Variances) in Standardized Residual Principal Components Analysis (PCA)
  3. More about Critical Eigenvalue Sizes (Variances) in Standardized-Residual Principal Components Analysis (PCA)
  4. Data Variance Explained by Rasch Measures
  5. PCA: Variance in Data Explained by Rasch Measures

Variance in Data Explained by Rasch Measures. Linacre, J.M. … Rasch Measurement Transactions, 2008, 22:1 p. 1164



Rasch Books and Publications
Invariant Measurement: Using Rasch Models in the Social, Behavioral, and Health Sciences, 2nd Edn. George Engelhard, Jr. & Jue Wang Applying the Rasch Model (Winsteps, Facets) 4th Ed., Bond, Yan, Heene Advances in Rasch Analyses in the Human Sciences (Winsteps, Facets) 1st Ed., Boone, Staver Advances in Applications of Rasch Measurement in Science Education, X. Liu & W. J. Boone Rasch Analysis in the Human Sciences (Winsteps) Boone, Staver, Yale
Introduction to Many-Facet Rasch Measurement (Facets), Thomas Eckes Statistical Analyses for Language Testers (Facets), Rita Green Invariant Measurement with Raters and Rating Scales: Rasch Models for Rater-Mediated Assessments (Facets), George Engelhard, Jr. & Stefanie Wind Aplicação do Modelo de Rasch (Português), de Bond, Trevor G., Fox, Christine M Appliquer le modèle de Rasch: Défis et pistes de solution (Winsteps) E. Dionne, S. Béland
Exploring Rating Scale Functioning for Survey Research (R, Facets), Stefanie Wind Rasch Measurement: Applications, Khine Winsteps Tutorials - free
Facets Tutorials - free		 Many-Facet Rasch Measurement (Facets) - free, J.M. Linacre Fairness, Justice and Language Assessment (Winsteps, Facets), McNamara, Knoch, Fan
Other Rasch-Related Resources: Rasch Measurement YouTube Channel
Rasch Measurement Transactions & Rasch Measurement research papers - free An Introduction to the Rasch Model with Examples in R (eRm, etc.), Debelak, Strobl, Zeigenfuse Rasch Measurement Theory Analysis in R, Wind, Hua Applying the Rasch Model in Social Sciences Using R, Lamprianou El modelo métrico de Rasch: Fundamentación, implementación e interpretación de la medida en ciencias sociales (Spanish Edition), Manuel González-Montesinos M.
Rasch Models: Foundations, Recent Developments, and Applications, Fischer & Molenaar Probabilistic Models for Some Intelligence and Attainment Tests, Georg Rasch Rasch Models for Measurement, David Andrich Constructing Measures, Mark Wilson Best Test Design - free, Wright & Stone
Rating Scale Analysis - free, Wright & Masters
Virtual Standard Setting: Setting Cut Scores, Charalambos Kollias Diseño de Mejores Pruebas - free, Spanish Best Test Design A Course in Rasch Measurement Theory, Andrich, Marais Rasch Models in Health, Christensen, Kreiner, Mesba Multivariate and Mixture Distribution Rasch Models, von Davier, Carstensen

To be emailed about new material on www.rasch.org
please enter your email address here:

I want to Subscribe: & click below
I want to Unsubscribe: & click below

Please set your SPAM filter to accept emails from Rasch.org

Rasch Measurement Transactions welcomes your comments:

Your email address (if you want us to reply):

If Rasch.org does not reply, please post your message on the Rasch Forum
 

ForumRasch Measurement Forum to discuss any Rasch-related topic

Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement

Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.

Coming Rasch-related Events
Apr. 21 - 22, 2025, Mon.-Tue. International Objective Measurement Workshop (IOMW) - Boulder, CO, www.iomw.net
Jan. 17 - Feb. 21, 2025, Fri.-Fri. On-line workshop: Rasch Measurement - Core Topics (E. Smith, Winsteps), www.statistics.com
Feb. - June, 2025 On-line course: Introduction to Classical Test and Rasch Measurement Theories (D. Andrich, I. Marais, RUMM2030), University of Western Australia
Feb. - June, 2025 On-line course: Advanced Course in Rasch Measurement Theory (D. Andrich, I. Marais, RUMM2030), University of Western Australia
May 16 - June 20, 2025, Fri.-Fri. On-line workshop: Rasch Measurement - Core Topics (E. Smith, Winsteps), www.statistics.com
June 20 - July 18, 2025, Fri.-Fri. On-line workshop: Rasch Measurement - Further Topics (E. Smith, Facets), www.statistics.com
Oct. 3 - Nov. 7, 2025, Fri.-Fri. On-line workshop: Rasch Measurement - Core Topics (E. Smith, Winsteps), www.statistics.com

 

The URL of this page is www.rasch.org/rmt/rmt221j.htm

Website: www.rasch.org/rmt/contents.htm