Critical Eigenvalue Sizes (Variances) in Standardized Residual Principal Components Analysis (PCA)

A principal components analysis PCA, of Rasch residuals, i.e., of observed responses minus their expectations, is used in Wright (1996) to investigate whether or not there is more than one variance component explaining the structure of respondent data. Wright postulates that, if the data are unidimensional, then components in the residuals will be at the noise level. Wright uses logit residuals. Linacre (1998) argues in favor of residuals standardized by their model standard deviation. These have the form of random normal deviates and will be adopted here.

The idea of retaining components that are above noise level is common practice in psychometrics. The Cattell (1966) scree test and the Kaiser (1960) rule are the most often used procedures to determine the number of components. They are both based on inspection of the correlation matrix eigenvalues. Cattell's recommendation is to retain only those components above the point of inflection on a plot of eigenvalues ordered by diminishing size. Kaiser (1960) recommends that only eigenvalues at least equal to one are retained. One is the average size of the eigenvalues in a full decomposition.

Smith and Miao (1994, p. 321) observe many components with eigenvalues greater than one in four simulations of unidimensional observational data. In their simulations, the first component corresponds to the Rasch dimension. The eigenvalue of the second component, the largest component in the random noise, never exceeds 1.40, suggesting that 1.40 is a threshold value for randomness.

Humphreys and Montanelli (1975) argue that the Kaiser rule is only true for very large correlation matrices. They propose that criterion eigenvalue thresholds be estimated by simulation studies based on random data formed into matrices of relevant sizes. The number of non-random components is determined by comparing the eigenvalue vector of the empirical data matrix with the vector of mean eigenvalues from the simulations. Only those leading empirical components with eigenvalues greater than their simulated equivalents are retained.

Table 1. Principal component eigenvalues of simulated correlation matrices
	N=100; L=20			N=500; L=30			N=1000; L=50			N=300; L=60
	5th	Mean	95th	5th	Mean	95th	5th	Mean	95th	5th	Mean	95th
1	1.74	1.90	2.07	1.42	1.48	1.55	1.42	1.46	1.50	1.92	2.00	2.09
2	1.61	1.72	1.85	1.37	1.42	1.47	1.38	1.42	1.45	1.85	1.91	1.98
3	1.50	1.59	1.69	1.33	1.36	1.40	1.35	1.38	1.41	1.79	1.84	1.91
4	1.39	1.47	1.56	1.29	1.32	1.36	1.33	1.35	1.38	1.73	1.78	1.83
5	1.29	1.37	1.46	1.25	1.29	1.32	1.31	1.33	1.35	1.68	1.73	1.78

Accordingly, simulations of normal random deviates are performed here. These approximate matrices of Rasch standardized residuals for situations in which the data fit the model. O'Connor's (2000) SAS program was used to efficiently perform multiple simulations.

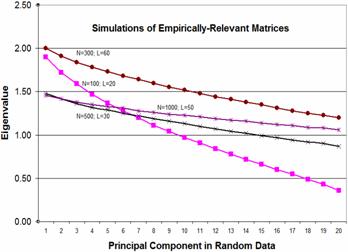
In Table 1, the average eigenvalues, along with their 5th and 95th percentile values, are presented, obtained from the simulation of different numbers of subjects (N) and items (L). The simulated data are all random noise. The graphs shows the Cattell scree plot for the eigenvalues of the first 20 components.

It is seen that the value of 1.40 is always exceeded by the first eigenvalue, and usually by the second. Consequently, the recommendation is to decide the criterion eigenvalue directly from relevant simulations.

Gilles Raîche
Université du Quèbec à Montréal
Département d'éducation et pédagogie

1. PCA: Data Variance: Explained, Modeled and Empirical
2. Critical Eigenvalue Sizes (Variances) in Standardized Residual Principal Components Analysis (PCA)
3. More about Critical Eigenvalue Sizes (Variances) in Standardized-Residual Principal Components Analysis (PCA)
4. Data Variance Explained by Rasch Measures
5. PCA: Variance in Data Explained by Rasch Measures

Cattell, R. B. (1966). The scree test for the number of factors. Multivariate Behavioral Research, 1, 629-637.

Kaiser, H. F. (1960). The application of electronic computers to factor analysis. Educational and Psychological Measurement, 20, 141-151.

Linacre, J. M. (1998). Detecting multidimensionality: which residual data-type works best? Journal of Outcome Measurement, 2, 3, 266-283.

Humphreys, L. G. and Montanelli, R. G. (1975). An examination of the parallel analysis criterion for determining the number of common factors. Multivariate Behavioral Research, 10, 193-206.

O'Connor BP (2000) SPS, SAS, and MATLAB programs for determining the number of components using parallel analysis and Velicer's MAP test. Behavior Research Methods, Instruments, and Computers, 32, 396-402.

Smith, R. M and Miao, C. Y. (1994). Assessing unidimensionality for Rasch measurement. In M. Wilson (Ed.): Objective Measurement: Theory into Practice. Volume 2. Greenwich: Ablex.

Wright, B.D. (1996) Local dependency, correlations and principal components. Rasch Meas Trans, 10, 3, 509-511.

Note: Tsair-Wei Chien reports that these findings can be replicated using the calculator at http://ires.ku.edu/~smishra/parallelengine.htm which is based on Patil, Vivek H., Surendra N. Singh, Sanjay Mishra, and Todd Donovan (2008). Efficient Theory Development and Factor Retention Criteria: A Case for Abandoning the 'Eigenvalue Greater Than One' Criterion, Journal of Business Research, 61 (2), 162-170.

Critical Eigenvalue Sizes (Variances) in Standardized Residual Principal Components Analysis, Raîche G. … Rasch Measurement Transactions, 2005, 19:1 p. 1012

Rasch Books and Publications
Invariant Measurement: Using Rasch Models in the Social, Behavioral, and Health Sciences, 2nd Edn. George Engelhard, Jr. & Jue Wang	Applying the Rasch Model (Winsteps, Facets) 4th Ed., Bond, Yan, Heene	Advances in Rasch Analyses in the Human Sciences (Winsteps, Facets) 1st Ed., Boone, Staver	Advances in Applications of Rasch Measurement in Science Education, X. Liu & W. J. Boone	Rasch Analysis in the Human Sciences (Winsteps) Boone, Staver, Yale
Introduction to Many-Facet Rasch Measurement (Facets), Thomas Eckes	Statistical Analyses for Language Testers (Facets), Rita Green	Invariant Measurement with Raters and Rating Scales: Rasch Models for Rater-Mediated Assessments (Facets), George Engelhard, Jr. & Stefanie Wind	Aplicação do Modelo de Rasch (Português), de Bond, Trevor G., Fox, Christine M	Appliquer le modèle de Rasch: Défis et pistes de solution (Winsteps) E. Dionne, S. Béland
Exploring Rating Scale Functioning for Survey Research (R, Facets), Stefanie Wind	Rasch Measurement: Applications, Khine	Winsteps Tutorials - free Facets Tutorials - free	Many-Facet Rasch Measurement (Facets) - free, J.M. Linacre	Fairness, Justice and Language Assessment (Winsteps, Facets), McNamara, Knoch, Fan
Other Rasch-Related Resources: Rasch Measurement YouTube Channel
Rasch Measurement Transactions & Rasch Measurement research papers - free	An Introduction to the Rasch Model with Examples in R (eRm, etc.), Debelak, Strobl, Zeigenfuse	Rasch Measurement Theory Analysis in R, Wind, Hua	Applying the Rasch Model in Social Sciences Using R, Lamprianou	El modelo métrico de Rasch: Fundamentación, implementación e interpretación de la medida en ciencias sociales (Spanish Edition), Manuel González-Montesinos M.
Rasch Models: Foundations, Recent Developments, and Applications, Fischer & Molenaar	Probabilistic Models for Some Intelligence and Attainment Tests, Georg Rasch	Rasch Models for Measurement, David Andrich	Constructing Measures, Mark Wilson	Best Test Design - free, Wright & Stone Rating Scale Analysis - free, Wright & Masters
Virtual Standard Setting: Setting Cut Scores, Charalambos Kollias	Diseño de Mejores Pruebas - free, Spanish Best Test Design	A Course in Rasch Measurement Theory, Andrich, Marais	Rasch Models in Health, Christensen, Kreiner, Mesba	Multivariate and Mixture Distribution Rasch Models, von Davier, Carstensen

Forum

Rasch Measurement Forum to discuss any Rasch-related topic

Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement

Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.

The URL of this page is www.rasch.org/rmt/rmt191h.htm

Website: www.rasch.org/rmt/contents.htm