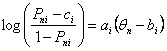
Fred Lord's three-parameter-logistic Item Response Theory (3-PL
IRT) model (Birnbaum, 1968) incorporates an item discrimination
parameter, modeling the slope of the item characteristic curve, and
a lower asymptote parameter modeling "guessing" or, better, "item
guessability". Here is a 3-PL model, written in log-odds format,
with ci as the lower asymptote, ai as the item
discrimination, θn as the person ability and
bi as the item difficulty:
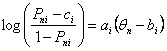 | (1) |
Lord's 4-PL model (Barton & Lord, 1981) incorporates an
upper asymptote parameter for item-specific "carelessness". Here is
a "carelessness" model, written in log-odds format, with
di as the upper asymptote:
| (2) |
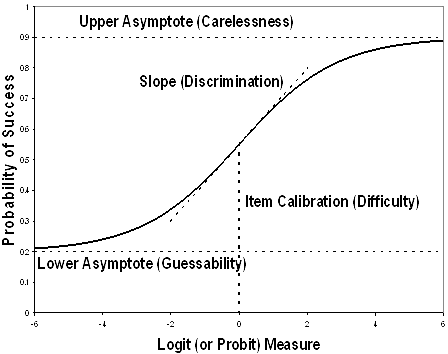 4-PL IRT Item Characteristic Curve |
Upper and lower asymptotes are notoriously difficult to estimate, so it appears that Lord abandoned his 4-PL model, and the value of ci in the 3-PL model is, on occasion, imputed from the number of options in a multiple-choice item, instead of being estimated directly from the data. Even the estimation of item discrimination usually requires constraints, such as "ai cannot be negative or too big."
The dichotomous Rasch model, however, provides an opportunity to estimate a first approximation to these parameters. These estimates can be useful in diagnosing whether the behavior they reflect could be distorting the Rasch measures. In the dichotomous Rasch model, ci=0, di=1 and ai=1. We can, however, treat the Rasch values as starting values in a Newton-Raphson iterative processed apparently intended to find the maximum-likelihood values of each of these parameters, in a context in which all other parameter values are known.
Following Wright & Masters (1982, 72-77), and using the standard approach of first and second derivatives of the log-likelihood of the data with respect to the parameter of interest, we obtain the following Newton-Raphson estimation equations for the first approximations:
Item discrimination (ICC slope):
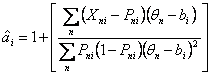 | (3) |
| with S.E. = 1/ sqrt ( | ) | (4) |
The Rasch expectation of ai is 1.
A corollary is that, when data fit the dichotomous Rasch model, there is zero correlation between the observation residuals and their generating measure differences.
There is a similar result for polytomous items. The Generalized
Partial Credit can be written:
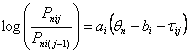 | (5) |
The "generalized" item discrimination (ICC slope), equivalent to a Rasch item discrimination index, is:
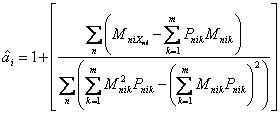 | (6) |
| where | and Mni0 = 0 | (7) |
And for the discrimination of polytomous inter-category
"generalized" thresholds:
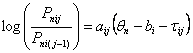 | (8) |
the "generalized" threshold discrimination is:
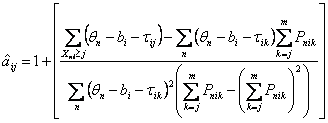 | (9) |
Returning to the dichotomous model, the lower asymptote (guessability) is:
 | (10) |
where 0 <= ci <= 1
| with S.E. = 1/ sqrt | 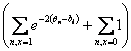 | (11) |
The Rasch expectation of ci is 0.
The upper asymptote (carelessness) is:
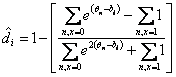 | (12) |
where 0 <= di <= 1
| with S.E. = 1/ sqrt | 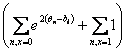 | (13) |
The Rasch expectation of di is 1.
In practice, it is convenient to use only observations in the lower tail for estimating the lower asymptote, in the center for estimating discrimination, and in the upper tail for estimating the upper asymptote.
John Michael Linacre
Birnbaum A. (1968) Some latent trait models and their uses in inferring an examinee's ability. In F.M. Lord & M.R. Novick, Statistical theories of mental test scores (pp. 395-479). Reading, MA: Addison-Wesley.
Barton M.A. & Lord F.M. (1981) An upper asymptote for the three-parameter logistic item-response model. Princeton, N.J.: Educational Testing Service.
Discrimination, Guessing and Carelessness Asymptotes: Estimating IRT Parameters with Rasch.
Linacre J.M. … Rasch Measurement Transactions, 2004, 18:1 p.959-960Discrimination, Guessing and Carelessness Asymptotes: Estimating IRT Parameters with Rasch, Linacre J.M. … Rasch Measurement Transactions, 2004, 18:1 p.959-960
| Forum | Rasch Measurement Forum to discuss any Rasch-related topic |
Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement
Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.
| Coming Rasch-related Events | |
|---|---|
| Jan. 16 - Feb. 13, 2025, Fri.-Fri. | On-line workshop: Rasch Measurement - Core Topics (E. Smith, Winsteps), www.statistics.com |
| Apr. 8 - Apr. 11, 2026, Wed.-Sat. | National Council for Measurement in Education - Los Angeles, CA, ncme.org/events/2026-annual-meeting |
| Apr. 8 - Apr. 12, 2026, Wed.-Sun. | American Educational Research Association - Los Angeles, CA, www.aera.net/AERA2026 |
| May. 15 - June 12, 2026, Fri.-Fri. | On-line workshop: Rasch Measurement - Core Topics (E. Smith, Winsteps), www.statistics.com |
| June 19 - July 25, 2026, Fri.-Sat. | On-line workshop: Rasch Measurement - Further Topics (E. Smith, Winsteps), www.statistics.com |
The URL of this page is www.rasch.org/rmt/rmt181b.htm
Website: www.rasch.org/rmt/contents.htm